La física se enfrenta día a día a algunos de los problemas más complejos y complicados de la humanidad. Algunos de ellos son tan basicos como conocer el movimiento preciso de los electrones en átomos pesados o predecir con total precisión el movimiento de los planetas del Sistema Solar. Para que estos problemas puedan solucionarse con la tecnología actual, los físicos utilizan modelos y aproximaciones. De todas las aproximaciones que se hacen, probablemente la más curiosa sea la de inventar partículas, o cuasipartículas.

En particular los problemas más complejos son aquellos que involucran muchos objetos que se afectan mutuamente. Como el problema de los planetas en los que cada uno de los planetas hace una contribución sobre el movimiento de los demás y este movimiento de los demás modifica el movimiento del primer planeta que a su vez… ¿Veis por dónde vamos, no? En la física del estado sólido (la parte que se encarga de entender las propiedades de la materia) estos problemas son el pan de cada día, por lo que las simplificaciones son muy bienvenidas.

Qué son las cuasipartículas

En física del estado sólido hay muchas situaciones en las que estudiar un propiedad de los materiales significa estudiar el movimiento de miles de billones de billones de electrones o átomos y la cosa puede ser complicada. Para eso, se inventa uno un modelo, en el cual las propiedades se explican mediante una partícula totalmente inexistente y ficticia: una cuasipartícula. Estas cuasipartículas permiten reducir el tamaño de las ecuaciones y simplificar el análisis.

Pongamos un ejemplo para entender estas cuasipartículas. La conducción eléctrica en los materiales se debe a los electrones que se encuentran en los niveles energéticos más elevados. Cuando estos niveles están casi completamente llenos, el número de electrones a estudiar es muy grande, porque hay pocos huecos. Entonces uno se imagina que los huecos son una cuasipartícula con carga igual a la del electrón, pero positiva.

Como el número de huecos es mucho menor que el de electrones, uno estudia el número de estas cuasipartículas (huecos) como si fueran particulas reales en un mar de electrones. El resultado es el mismo que estudiar el movimiento de todos los electrones, pero mucho más rápido de obtener. Es como si para explica cómo funciona la gravedad en una botella de agua cerrada, en vez de estudiar el agua, estudiáramos el movimiento de la burbuja de agua, que sería nuestra cuasipartícula.

Antes de serguir, hay que hacer una aclaración. Las cuasipartículas no son partículas, son inventos, entes matemáticos que ayudan a estudiar y resolver problemas. No debemos confundir las cuasipartículas con las partículas virtuales que son partículas que se crean y se destruyen en el vacío constantemente, como os contamos hace un tiempo.

Para qué sirven las cuasipartículas, ejemplos

Como acabamos de ver, las cuasipartículas son entes matemáticos que los físicos utilizan para simplificar el análisis y poder obtener resultados sobre las propiedades de los materiales. Pero los huecos no son las únicas cuasipartículas, existen muchas otras como los plasmones, para modelizar el plasma, los excitones para modelar las excitaciones de las redes cristalinas…

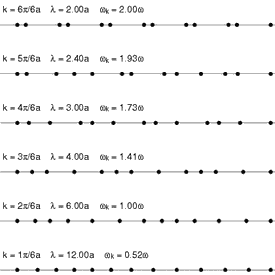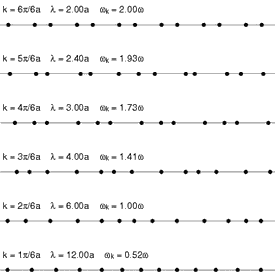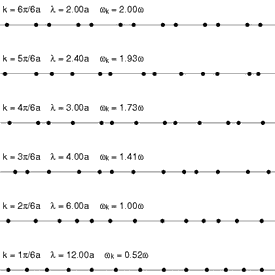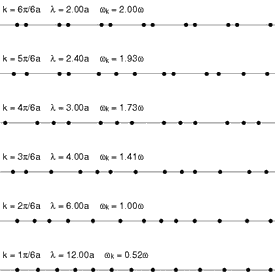
Vibraciones que pueden modelarse como el paso de un fonón

De todos estos mi segundo ejemplo favorito (después de los huecos) es el de los fonones. Los fonones son cuasipartículas que dan cuenta de las vibraciones de los átomos dentro de los materiales. Estas vibraciones son similares a las que se producen en el aire cuando hablamos y por analogía de la ondas de sonido con las de luz se llaman fonones, en una clara referencia a los fotones de la luz.

Con estas cuasipartículas podemos entender mejor la difusión del sonido en sólidos y propiedades como los colores que absorben, cómo conducen el calor o la electricidad en su interior e incluso por qué algunos materiales pueden ser superconductores y otros no. Todo eso analizado gracias al uso de partículas que no existen, ¿no es increíble?